深度学习教程 | 深层神经网络

人工智能神经网络深度学习前向传播反向传播激活函数

发布于 6 个月前

标题：如何使用ShowMeAI进行图像处理和分析教程

作者：韩信子@ShowMeAI

教程网址：www.showmeai.tech/tutorials/3…

地址：www.showmeai.tech/article-det…

收藏ShowMeAI查看更多精彩内容

引言

在ShowMeAI之前的一篇文章中，我们对浅层神经网络进行了介绍。文章包括了以下主要内容:

- 神经网络的基本结构，即输入层、隐藏层和输出层。

- 浅层神经网络的前向传播和反向传播过程。

- 神经网络参数的梯度下降优化方法。

- 不同激活函数的优点与缺点以及非线性性的原因。

- 参数随机初始化的方式。

本篇内容将探讨深层神经网络。

我们已经提到过浅层神经网络。现在，让我们来谈谈更深的神经网络——深层神经网络，它实际上是由多个隐藏层构成的神经网络。下面，我们将展示不同深度的神经网络模型：

1. **浅层神经网络**：这种类型的神经网络只包含一个或几个隐藏层。

2. **中层神经网络**：这类网络增加了两个或更多隐藏层。

3. **深层神经网络**：这包括了更多的隐藏层，进一步提升了模型的学习能力和复杂性。

我们将采用「层数」和「输出层」作为命名方式。例如，逻辑回归可以被称作 1 层 NN，单层神经网络则为 2 层 NN，而拥有两个隐藏层的神经网络就称为 3 层 NN。以此类推。因此，在提及 L 层 NN 时，指的是包含 L-1 层隐藏层的神经网络。

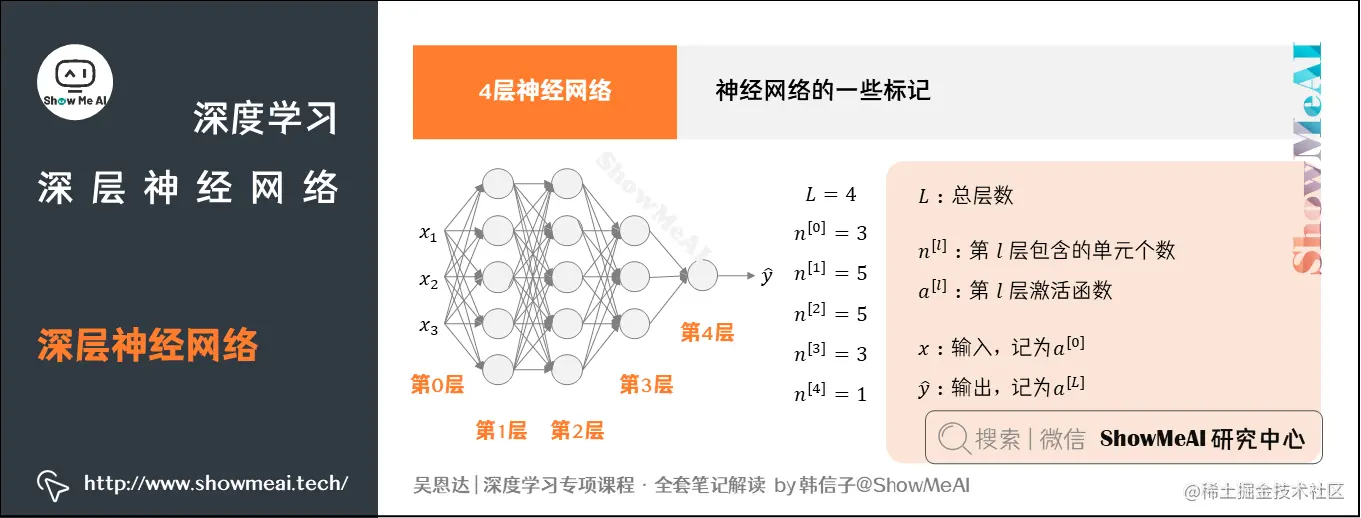
接下来，让我们了解一下一些关于神经网络的标记写法。以图中所示的 4 层神经网络为例：

1. 隐层个数：这里的隐层是指神经网络内部具有非线性变换作用的部分，其功能是将输入向量转化为更复杂的表达形式。

2. 输出层：输出层负责接收隐藏层传递过来的信息，并通过激活函数将其转换为可解释的输出结果。

这些标记不仅帮助我们清晰地描述神经网络结构，还能在代码实现和模型训练时提供必要的信息。

### ① 总层数用LLL表示，L=4

输入层是第0层，输出层是第LL层。\[ \text{Layer count: } L = 4 \]

输入层的维度 $ n[0] = nx = 3 $ 表示输入特征的数量。

### ② n[l]n^{[l]}n[l]表示第lll层包含的单元个数，l=0,1,⋯ ,L

下图模型中，\[ n[0] = n_x = 3 \]，表示三个输入特征 $ x_1, x_2, x_3 $。

下图模型中\[ n[1]=5, n[2]=5, n[3]=3, n[4]=n[L]=1\]。

- 第1层有5个单元，第2层和第3层各有5个单元，第4层（输出层）有一个单元。

### ③ 第lll层的激活函数输出用a[l]a^{[l]}a[l]表示，a[l]=g[l](z[l])

在第lll层，\[ a[l] = g^{[l]}(z^{[l]}) \] 表示激活函数的输出。\[ g[l] \] 和 $ z^{[l]} $ 分别是激活函数和输出值。

### ④ W[l]W^{[l]}W[l]表示第lll层的权重，用于计算z[l]

\[ W^{[l]} \] 是第lll层的权重矩阵。它用于将输入特征 $ a[l-1] $ 转换为输出 $ z[l] $。

### ⑤ 输入xxx记为a[0]a^{[0]}a[0]

在神经网络中，$ x_1, x_2, x_3 $ 等输入特征被表示为 $ a[0] = [x_1, x_2, x_3]^T $.

### ⑥ 输出层y^\hat yy^记为a[L]a^{[L]}a[L]

输出层的激活函数输出是\[ y^{\hat{}} = a[L] \]。

### 2.1 单个样本的计算

对于单个样本，我们有：

\[ y = f(\mathbf{w}^T \mathbf{x} + b) \]

其中：

- $y$ 是输出结果。

- $f$ 是激活函数。

- $\mathbf{w}$ 是权重向量。

- $\mathbf{x}$ 是输入向量。

- $b$ 是偏置项。

具体步骤如下：

1. 将输入向量 $\mathbf{x}$ 与权重向量 $\mathbf{w}$ 进行内积运算，得到一个标量值 $\mathbf{w}^T \mathbf{x}$。

2. 在加偏置项 $b$ 后，得到的值加上 $\mathbf{w}^T \mathbf{x}$，即为输出结果 $y$。

这个过程可以表示为：

\[ y = f(w_1 x_1 + w_2 x_2 + ... + b) \]

### 2.2 深层神经网络的前向传播计算

对于深层神经网络，我们可以进一步推导其前向传播的具体步骤。以一个包含4层神经元的网络为例：

#### 第一层：输入层

假设输入为 $ \mathbf{x} = [x_1, x_2] $。

#### 第二层：隐藏层

假设每层有 $n$ 个神经元，权重向量为 $\mathbf{w}_j$, 偏置项为 $b_j$。输出值为 $y_i$：

\[ y = f(w_{1j} x_1 + w_{2j} x_2 + b_j) \]

#### 第三层：隐藏层

同上，权重向量和偏置项分别为 $w_{3j}$ 和 $b_j$。输出值为 $y_i$：

\[ y = f(w_{1j} y_{i-1} + w_{2j} x_2 + b_j) \]

#### 第四层：输出层

假设权重向量和偏置项为 $w_{4j}$ 和 $b_j$。最终输出值为：

\[ y = f(w_{1j} y_{i-1} + w_{2j} y_{i-1} + b_j) \]

这个过程可以总结为：

\[ y = f(\sum_k w_{kj} y_{k-1} + b_j) \]

### 2.3 深层神经网络的前向传播计算过程

在深层神经网络中，前向传播过程可以概括如下：

#### 前向传播的基本步骤

1. **输入层**：接收原始数据 $x$。

2. **隐藏层**：

- 初始化权重和偏置项。

- 通过激活函数（如 ReLU）进行线性变换并加偏置项，得到中间输出 $y_{k-1}$。

3. **输出层**：

- 再次初始化权重和偏置项。

- 将上一层的输出与当前权重和偏置项相乘，并通过激活函数（如 softmax）进行非线性变换并加偏置项，得到最终的预测值 $y$。

这种层级结构允许深层神经网络捕捉更复杂的模式和特征。

2.2 m 个样本的批量计算

在这种情况下，我们将使用向量化的矩阵形式来进行并行计算：

- 对于 $ m $ 个训练样本，我们可以将它们组织成一个矩阵。

- 这些样本可以视为输入数据集的一部分。

例如，如果 $ m = 1000 $，那么我们有一个 1000 行的向量。每个样本可以看作是这个向量的一列。

这种处理方式适用于批量计算，因为它允许我们将所有样本一起处理，而不需要逐个处理它们。

在第lll层的前向传播过程中，可以表示为：

\[ Z[l] = W[l]A^{[l-1]} + b^{[l]} \]

\[ A[l] = g[l](Z[l]) \]

其中，对于每一层$ l $，从输入数据到输出之间的权重矩阵 $ W[l] $ 和偏置项 $ b[l] $ 表示为：

\[ Z[l] = W[l]A^{[l-1]} + b^{[l]} \]

\[ A[l] = g[l](Z[l]) \]

这种表达方式对于向量化形态下的矩阵维度处理更加简洁。

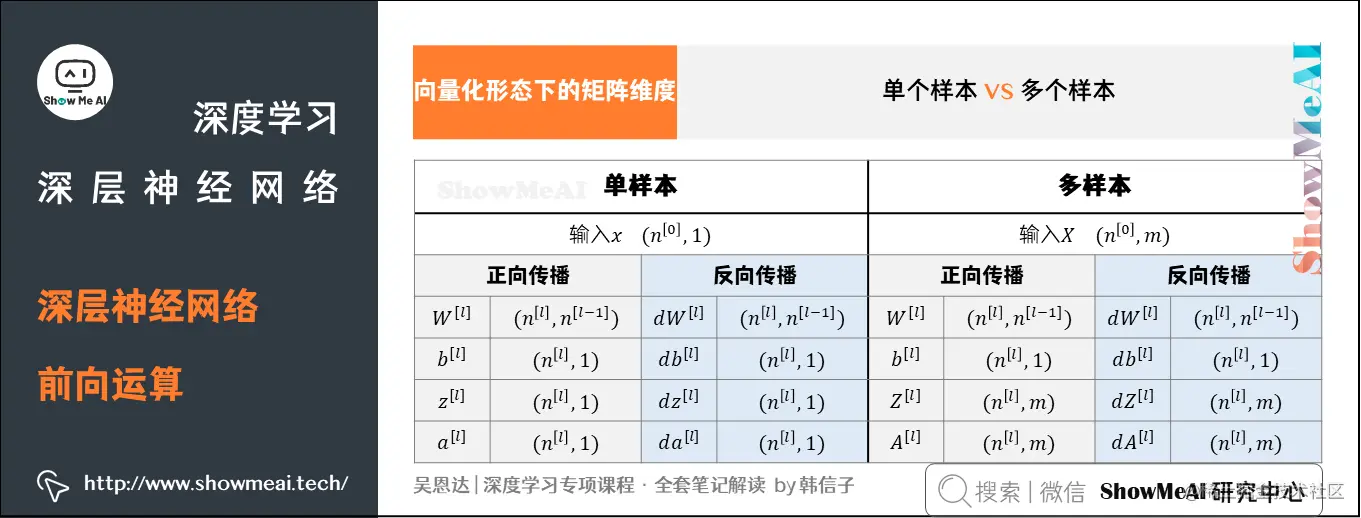
在单个训练样本的情况下，神经网络参数 $ W^l $ 和 $ b^l $，其维度分别为：

- **$ W^l $: (n_l, n_{l−1}) \)

- **$ b^l $: (n_l, 1) \)

其中，

\[ l = 1, \cdots, L \]

- $ n_l $ 和 $ n_{l−1} $ 分别表示第 $ l $ 层和 $ l−1 $ 层的单元个数。

- $ n_0 = nx $，表示输入层特征数目。

在反向传播过程中，计算梯度时需要用到的参数和梯度分别为：

- **$ dW^l $: (n_l, n_{l−1}) \)

- **$ db^l $: (n_l, 1) \)

注意到 $ W^l $ 和 $ dW^l $ 的维度相同，而 $ b^l $ 和 $ db^l $ 的维度也相同。这使得在计算梯度和更新参数时更加方便。

在正向传播过程中，激活函数的输出 $ z[l] $ 和输入 $ a[l] $ 的维度分别为：

- **$ z[l]: (n_l, 1) $

- **$ a[l]: (n_l, 1) $**

同样地，梯度 $ dz^l $ 和 $ da^l $ 的维度与激活函数的输入和输出维度相同。

对于mmm个训练样本，输入矩阵XXX的维度是(n[0],m)(n^{[0]},m)(n[0],m)。需要注意的是W[l]W^{[l]}W[l]和b[l]b^{[l]}b[l]的维度与只有单个样本是一致的：

- W[l]: (n[l],n[l−1])W^{[l]}:\ (n^{[l]},n^{[l-1]})W[l]:(n[l],n[l−1])

- b[l]: (n[l],1)b^{[l]}:\ (n^{[l]},1)b[l]:(n[l],1)

只不过在运算Z[l]=W[l]A[l−1]+b[l]Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}Z[l]=W[l]A[l−1]+b[l]中，b[l]b^{[l]}b[l]会被当成(n[l],m)(n^{[l]},m)(n[l],m)矩阵进行运算，这是基于python numpy的广播特性，且b[l]b^{[l]}b[l]每一列向量都是一样的。

dW[l]dW^{[l]}dW[l]和db[l]db^{[l]}db[l]的维度分别与W[l]W^{[l]}W[l]和b[l]b^{[l]}b[l]的相同。

不过，Z[l]Z^{[l]}Z[l]和A[l]A^{[l]}A[l]的维度发生了变化：

- Z[l]: (n[l],m)Z^{[l]}:\ (n^{[l]},m)Z[l]:(n[l],m)

- A[l]: (n[l],m)A^{[l]}:\ (n^{[l]},m)A[l]:(n[l],m)

dZ[l]dZ^{[l]}dZ[l]和dA[l]dA^{[l]}dA[l]的维度分别与Z[l]Z^{[l]}Z[l]和A[l]A^{[l]}A[l]的相同。

4.为什么需要深度网络

当今大家看到的很多AI智能场景背后都是巨大的神经网络在支撑。强大能力很大一部分来源于神经网络足够“深”，也就是说随着网络层数增多，神经网络就更加复杂参数更多，学习能力也更强。下面是一些典型的场景例子说明。

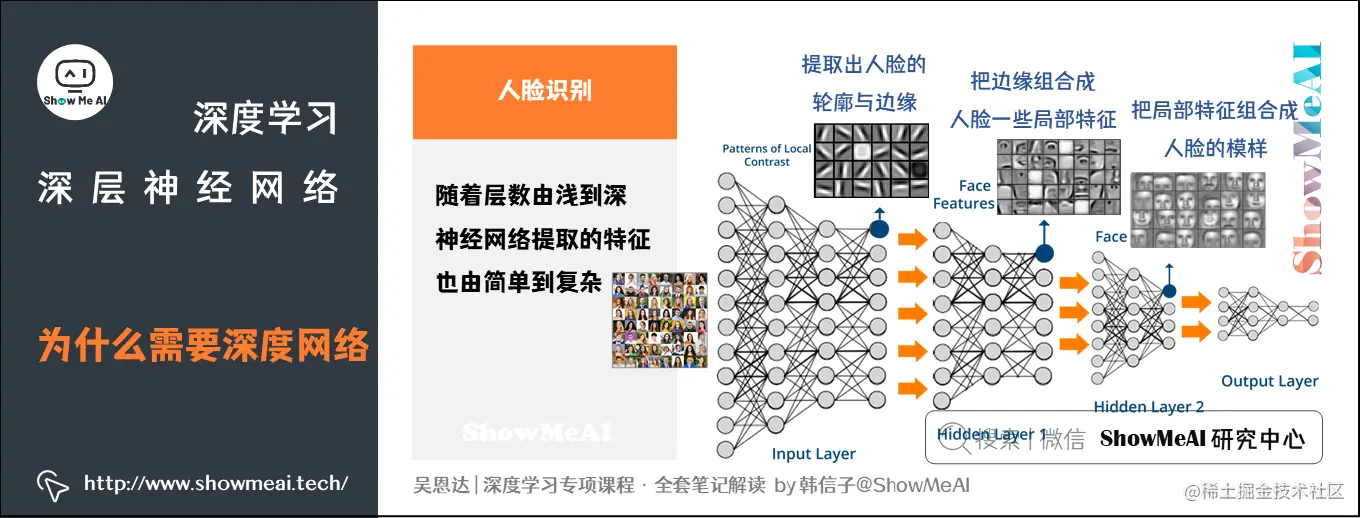
4.1 人脸识别例子

如下图所示的人脸识别场景，训练得到的神经网络，每一层的作用有差别：

第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘，即边缘检测。这样每个神经元得到的是一个边缘信息。

第二层所做的事情就是将前一层的边缘进行组合，组合成人脸的一些局部特征，比如眼睛、鼻子、嘴巴等。

后续层次逐层把这些局部特征组合起来，融合成人脸的模样。

可以看出，随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。隐藏层越多，能够提取的特征就越丰富、越复杂，模型的准确率也可能会随之越高。详细的CNN应用：人脸识别和神经风格转换

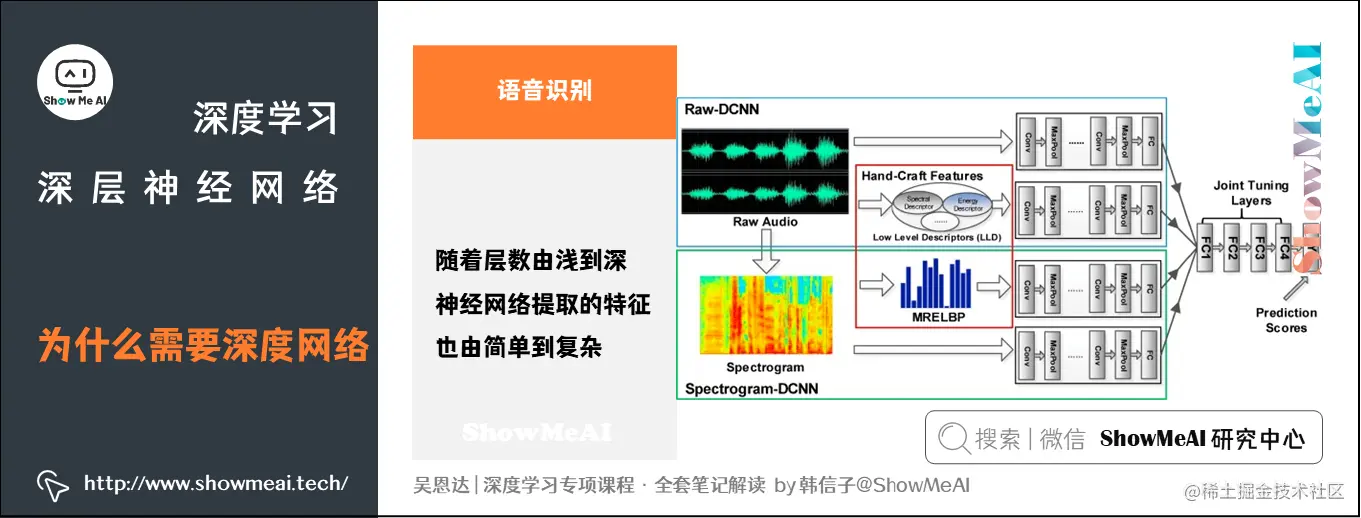
语音识别模型同样遵循这一原理：

浅层的神经元能检测简单的音调

较深的神经元能检测出基本的音素

更深的神经元能检测出单词信息

网络足够深的话，还能对短语、句子进行检测。

4.3 深度网络的其他优势

除学习能力与特征提取强度之外，深层网络还有另一个优点，那就是能够减少神经元的数量。这使得计算量大大降低。

举一个例子来说明这一点：使用电路理论，可以计算逻辑输出：

$$y = x_1 \oplus x_2 \oplus x_3 \oplus \cdots \oplus x_n$$

这里的 $$\oplus$$ 表示“异或”操作。

对于这个逻辑运算，如果通过深度网络完成，每层将前一层的两两单元进行异或，最终得到一个输出。例如：

输入：$x_1 = 0, x_2 = 1$

第一层：$y_1 = (x_1 \oplus x_2) = 1$

输入：$x_1 = 1, x_2 = 0$

第二层：$y_2 = (x_1 \oplus x_2) = 1$

输入：$x_1 = 0, x_2 = 0$

第三层：$y_3 = (x_1 \oplus x_2) = 0$

通过这样的方式，整个深度网络的层数为 $\log_2(n)$（不包含输入层），总共使用的神经元个数为：

1+2+\cdots+(2^{log_2(n)-1})=1\cdot\frac{1-2^{log_2(n)}}{1-2}=2^{log_2(n)}-1=n-1

可以看出，输入的数量是 $n$，而这种深度网络所需的神经元数量仅为 $n-1$。

如果不用深层网络，仅仅使用单个隐藏层，如上右图所示，由于包含了所有的逻辑位(0和1)，那么需要的神经元个数O(2n)O(2^n)O(2n)是指数级别的大小。

对于其他场景和问题也一样，处理同样的逻辑问题，深层网络所需的神经元个数比浅层网络要少很多。这也是深层神经网络的优点之一。

尽管深度学习有着非常显著的优势，吴恩达老师还是建议对实际问题进行建模时，尽量先选择层数少的神经网络模型，这也符合奥卡姆剃刀定律(Occam’s Razor)。对于比较复杂的问题，再使用较深的神经网络模型。

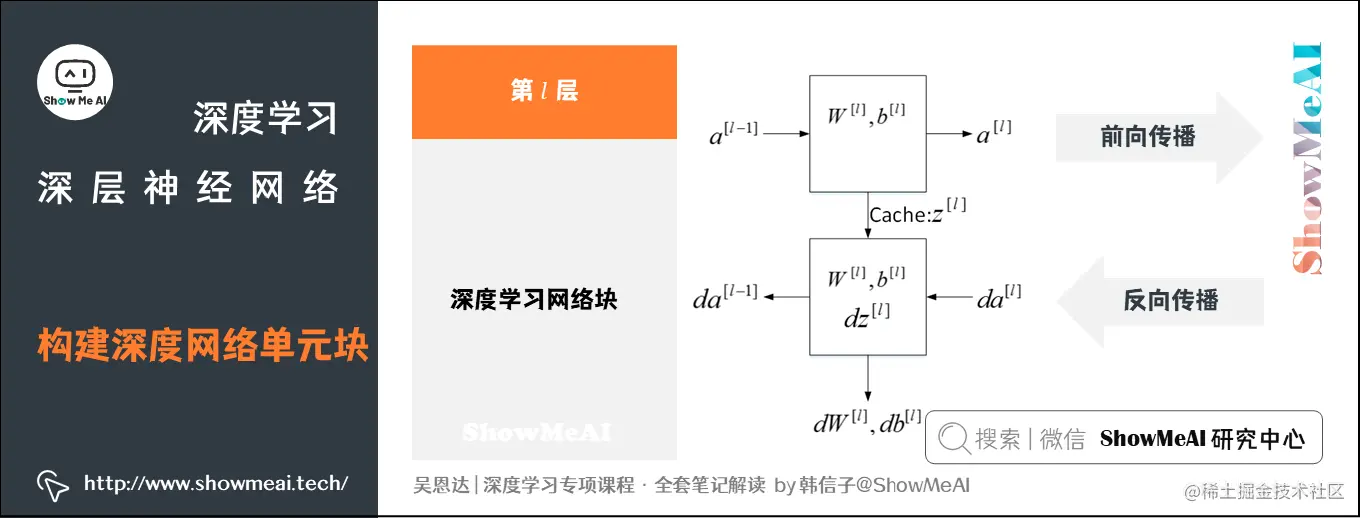
下面用流程块图来解释神经网络前向传播和反向传播过程。

如图所示，对第 l 层而言，在前向传播过程中，我们有：

输入：a[l−1] a^{[l-1]} a[l−1]

输出：a[l] a^{[l]} a[l]

参数：W[l] W^{[l]} W[l]、b[l] b^{[l]} b[l]

缓存变量：z[l] z^{[l]} z[l]

在反向传播过程中：

输入：da[l] da^{[l]} da[l]

输出：da[l−1] da^{[l-1]} da[l−1]、dW[l] dW^{[l]} dW[l]、db[l] db^{[l]} db[l]

参数：W[l] W^{[l]} W[l]、b[l] b^{[l]} b[l]

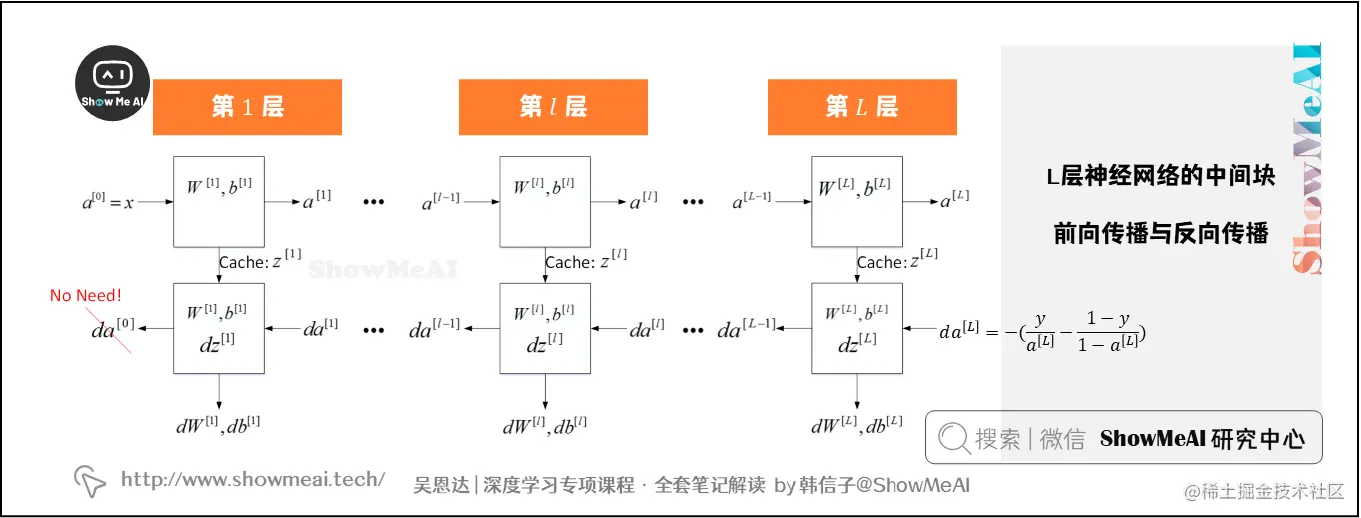
这是第 l 层的流程块图。对于神经网络的所有层，整体的前向传播和反向传播过程如下所示：

- 前向传播过程：

- 输入通过激活函数得到输出。

- 参数更新并计算缓存变量 z[l]。

- 反向传播过程：

- 对于每一层，输入通过参数更新后得到输出，然后进行梯度的反向传递。

- 更新每个层的梯度，并使用这些梯度来更新权重和偏置。

6.前向传播与反向传播

我们继续接着上一部分流程图的内容，推导神经网络的正向传播和反向传播的具体表达式。

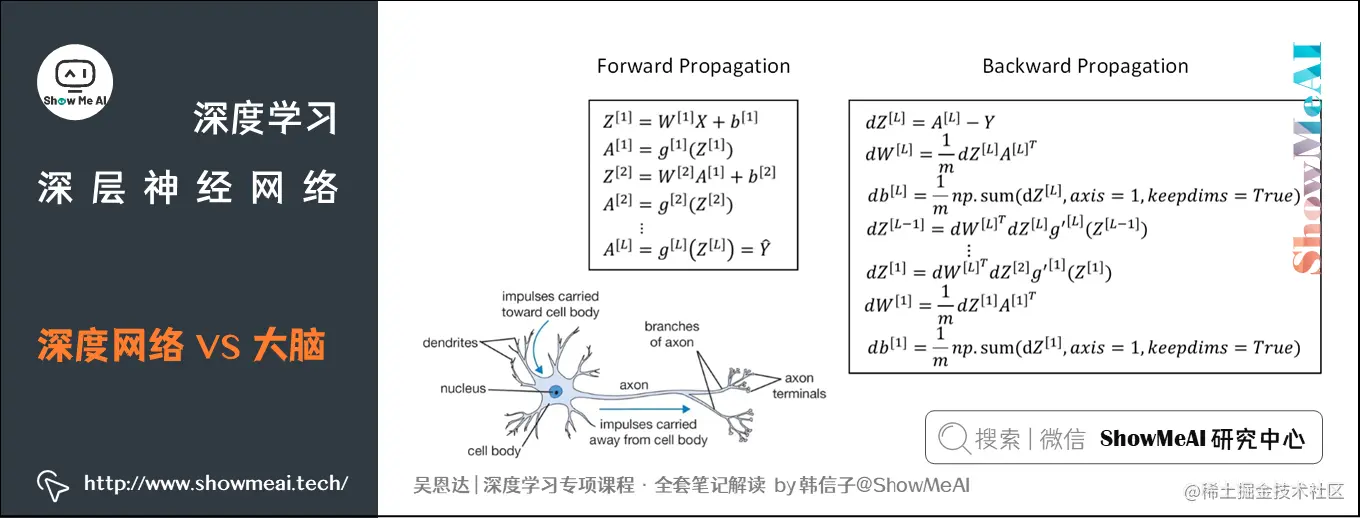
### 6.1 前向传播过程

令层数为第l层，输入是a[l-1]，输出是a[l]，缓存变量是z[l]。其数学表达式如下：

\[ z^{[l]} = W^{[l]} a^{[l-1]} + b^{[l]}, \quad a^{[l]} = g^{[l]}(z^{[l]}) \]

其中：

- $a^{[l-1]}$ 是第l-1层的输出。

- $W^{[l]}$ 是第l层的权重矩阵。

- $b^{[l]}$ 是第l层的偏置项。

### 6.2 反向传播过程

输入是da[l]，输出是da[l-1]、dW[l]和db[l]。其数学表达式如下：

\[ dz^{[l]} = da^{[l]} \cdot g^{[l]\prime}(z^{[l]}), \quad dW^{[l]} = dz^{[l]} \cdot a^{[l-1]}, \quad db^{[l]} = dz^{[l]} \]

\[ da^{[l-1]} = W^{[l]T} \cdot dz^{[l]}, \quad dz^{[l+1]} = W^{[l+1]T} \cdot dz^{[l+1]} \cdot g^{[l]\prime}(z^{[l]}), \quad dZ^{[l]} = dA^{[l-1]} \cdot g^{[l]\prime}(Z^{[l]}), \quad Z^{[l]} = W^{[l]T} \cdot dz^{[l]}, \]

其中：

- $dz^{[l+1]}$ 是第l层的输出关于输入的梯度。

- $dA^{[l-1]}$ 是第l-1层的输出关于输入的梯度。

### 7. 参数与超参数

在训练过程中，需要对神经网络的权重和偏置进行学习调整。这些调整通常通过优化算法（如梯度下降、Adam等）来进行。同时，还有许多超参数也需要设置，包括学习率、批量大小、迭代次数等，以确保模型性能的优化。

以上内容涵盖了正向传播和反向传播的基本原理及其在实际应用中的具体表现形式。

在神经网络中，有两个关键的概念：参数（parameters）和超参数（hyperparameters）。这些概念之间的区别非常重要。

1. **参数（Parameters）**：

- 在神经网络的计算过程中，我们经常提到W[l]W^{[l]}W[l]和b[l]b^{[l]}b[l]。这里，W[l]代表第l层中所有神经元的权重矩阵，而b[l]则是每层的偏置项。

- 这些参数决定了网络在训练过程中如何更新其内部连接。

2. **超参数（Hyperparameters）**：

- 超参数是一个预先确定但不会直接影响计算过程中的具体值。它们包括学习率α\alphaα，训练迭代次数NNN，神经网络的层数LLL以及每个层中神经元的数量n[l]n^{[l]}n[l]。

- 学习率α\alphaα决定了更新参数W[l]W^{[l]}W[l]和b[l]b^{[l]}b[l]的速度。训练迭代次数NNN则指定了网络在学习过程中总共需要进行多少次更新操作。

- 神经网络的层数LLL以及每个层中神经元的数量n[l]n^{[l]}n[l]决定了网络的整体架构和复杂度。

超参数的选择对于优化神经网络的表现至关重要。它们的影响范围从全局参数调整到具体的局部优化过程，因此需要谨慎选择。

设置最优超参数是一个需要经验知识和复杂计算的问题。通常，做法是选择一个固定范围内的超参数值，然后代入神经网络进行训练，并测试成本函数随着迭代次数增加的变化情况。根据结果来决定哪一组超参数对应于成本函数的最小化。

这类似于机器学习中的实验验证方法。关于模型评估，请参见 ShowMeAI文章：图解机器学习 | 模型评估方法与准则

9.神经网络vs人脑

神经网络和人脑在处理信息的方式上有一些相似之处，但它们也有很大的不同点。神经网络通过执行多层的计算来完成任务，而人的大脑则通过大量的经验积累和反馈调节来改进其行为。

尽管两者都涉及复杂的计算过程，但它们的工作方式完全不同。

神经网络与人脑机制之间的联系如何？它们之间有多少相似之处呢？

这问题其实可以从多个角度来探讨：

首先，从功能层面来看，神经网络和大脑都是实现信息处理的方式之一。两者都涉及对环境刺激进行分析、编码、存储及输出的过程。

其次，在结构上，神经网络也与人脑结构类似。例如，人脑的神经元之间的连接类似于神经网络中的节点之间相互连接，而神经网络中使用的激活函数也可以理解为大脑中神经元激活的模型。

最后，从算法层面来看，虽然两者实现的方法不同，但它们在某种程度上也有相似性。比如深度学习就是在模仿人脑处理复杂信息的方式。

综上所述，神经网络与人脑机制之间确实存在一定的联系，且有很多相似之处。不过，这并不意味着它们完全相同，因为两者的实现方式、功能以及结构等都有所不同。

在前面我们看到，神经网络实际上可以分成两个部分：前向传播过程和反向传播过程。每个神经元采用激活函数的方式，类似于感知机模型。这种简化的人脑神经元模型与人脑神经元类似。

人脑神经元可分为树突、细胞体和轴突三部分。树突接收外界电刺激信号，传递给细胞体进行处理，最后由轴突传递给下一个神经元。

人脑的神经元结构和处理方式是极其复杂且难以完全理解的。虽然目前神经网络模型为我们提供了简化的人工智能实现，但关于如何在生物体内进行学习仍是一个未解之谜。

**参考资料**

1. 图解机器学习 | 模型评估方法与准则

2. ShowMeAI系列教程推荐

深度学习涉及众多技术和理论，请参阅以下资源：

- 图解Python编程：从入门到精通系列教程

- 图解数据分析：从入门到精通系列教程

- 图解AI数学基础：从入门到精通系列教程

- 图解大数据技术：从入门到精通系列教程

- 图解机器学习算法：从入门到精通系列教程

- 机器学习实战：手把手教你玩转机器学习系列

- 深度学习教程 | 吴恩达专项课程 · 全套笔记解读